
 |
Analog synthesis - VCO - SAW
We know dat a SAW wave contains all the harmonics in the following way:
| Harmonic | Amplitude (or "loudness") |
| 1st | 1 |
| 2nd | 1/2 |
| 3rd | 1/3 |
| 4th | 1/4 |
| 5th | 1/5 |
| 6th | 1/6 |
| 7th | 1/7 |
| ... | ... |
And so on.
Now that you know the harmonics of a SAW wave, you can try to create a sound, using only SINE waves. SINE waves do not have any harmonics (only the first, which is the note you pressed on the keyboard), they are very "pure". That's why you use this pure wave form to approximate the sound of a SAW wave. You make a sine wave of every harmonic in the table, and add them up. You just follow the rules: start with a sine for the first harmonic, then add the second harmonic with a sine, that is double as fast, but half the amplitude, and add them to each other.
The next step is to add the 3rd harmonic, one third of the amplitude, and add this wave to the previous two.
And see what happens.
STEP 1:
-
create a sine wave
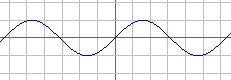 sin(x)
sin(x)
STEP 2:
-
create a sine wave twice the speed and half the loudness
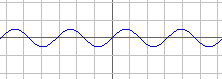 sin(2x)/2
sin(2x)/2
- merge the two wave forms in one graph
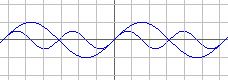
- take the sum of both waves and observe the resulting wave
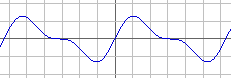 sin(x) + sin(2x)/2
sin(x) + sin(2x)/2
STEP 3:
- create a sine wave three times the speed, a third of the loudness
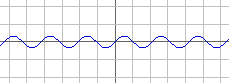 sin(3x)/3
sin(3x)/3
- merge the three wave forms in one graph
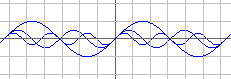
- take the sum of the three waves and observe the resulting wave
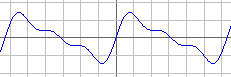 sin(x) + sin(2x)/2 + sin(3x)/3
sin(x) + sin(2x)/2 + sin(3x)/3
STEP 4:
- create a sine wave four times the speed, a fourth of the loudness
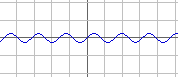 sin(4x)/4
sin(4x)/4
- merge the four wave forms in one graph
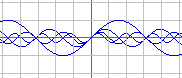
- take the sum of the four waves and observe the resulting wave
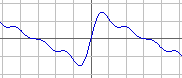 sin(x) + sin(2x)/2 + sin(3x)/3 + sin(4x)/4
sin(x) + sin(2x)/2 + sin(3x)/3 + sin(4x)/4
Now you see it happen quite clearly: an approximate SAW wave. Made with only SINE waves! When you go on adding waves of 5, 6, 7 the speed and a 5th, 6th, 7th of the loudness, you will see a SAW developing better and better.
Reasoning backwards: this also means that when a synthesizer has a SAW-oscillator (and they all do), you also know that this saw wave contains all the harmonics. The higher the harmonic, the softer the loudness of the harmonic gets (see table on top of page).
The graphs are made with the free "Power Toy Calc" for WinXP from Microsoft.